Para que un objeto se encuentre en equilibrio, es necesario que cumpla con dos condiciones denominadas Primera y Segunda condición de equilibrio. De acuerdo con la segunda ley de Newton, la suma de las fuerzas (denominada fuerza neta) que actúan sobre un cuerpo debe ser cero si el objeto se encuentra en reposo. En consecuencia, la Primera condición de equilibrio establece que:
Sin embargo, la fuerza neta sobre un objeto puede ser cero y aún así puede actuar sobre él una torca o momento que lo haga moverse. Observemos la Figura 1.
 |
Figura 1. Aún cuando la fuerza neta sobre la regla es cero, el par de fuerzas de igual magnitud pero que actúan en diferentes puntos del cuerpo y en direcciones contrarias hacen que la regla gire. |
De acuerdo con esta observación, se establece que para que un cuerpo se mantenga en reposo debe cumplir también que la suma de todas las torcas o momentos que actúen sobre él debe ser cero, de esta forma se llega a la Segunda condición de equilibrio que establece que:
Esta condición garantiza que la aceleración angular en torno a cualquier eje sea cero y además si el objeto no está inicialmente en rotación, no girará a menos que se modifique esta condición.
Para reforzar lo explicado hasta ahora, se compartirá un problema ya resuelto:
PROBLEMA
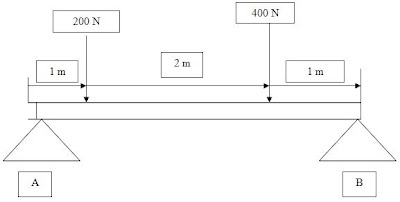
Una viga de 4 m de longitud soporta dos cargas, una de 200 N y otra de 400 N como se ve en la figura. Determinar los esfuerzos de reacción a que se encuentran sujetos los apoyos, considere despreciable el peso de la viga.
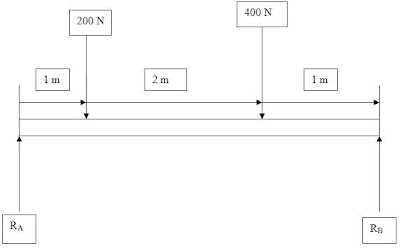
Cambiándolo a diagrama de cuerpo libre:
RESOLUCIÓN
Para que la viga esté en equilibrio de traslación y de rotación tenemos que:
Aplicando la primera condición de equilibrio tenemos:
ΣF = 0 = RA + RB + (-F1)+ (-F2)= 0…….. (1)
ΣF = 0= RA + RB = F1 + F2
ΣF = RA + RB = 200 N + 400 N
ΣF = RA + RB = 600 N ecuación 1.
Aplicando la segunda condición de equilibrio y eligiendo el soporte A tenemos:
ΣMA= RB (4 m)- 400 N (3 m) – 200 N (1 m) = 0
ΣMA= RB (4 m)- 1200 N.m-200 N.m = 0
ΣMA= RB (4 m)- 1400 N.m= 0
ΣMA= RB (4 m)= 1400 N.m.
Despejando RB tenemos:
RB = 1400 N.m = 350 N
4 m
Sustituyendo el valor de RB en la ecuación 1 para hallar RA tenemos:
RA = 600 N - RB
RA = 600 N – 350 N = 250 N
Otro punto que se debe recordar es que matemáticamente, para el caso de fuerzas coplanares, se debe cumplir que la suma aritmética de los momentos relacionados con rotaciones antihorarias debe ser igual a la suma aritmética de los momentos relacionados con rotaciones horarias, como se puede observar en la fig. 2:
 |
| Figura 2 |
En general, un cuerpo se encontrará en equilibrio traslacional y equilibrio rotacional cuando se cumplen las dos condiciones de equilibrio.
A continuación, se muestra un problema con su respectiva solución utilizando la ecuación anterior:
PROBLEMA
Si la barra homogénea de 4 Kg de masa se encuentra en equilibrio en la forma que se indica. Determinar la tensión de la cuerda vertical (considerar: g = 10 m/s2).
Si la barra homogénea de 4 Kg de masa se encuentra en equilibrio en la forma que se indica. Determinar la tensión de la cuerda vertical (considerar: g = 10 m/s2).
RESOLUCIÓN
Hagamos DCL de la barra teniendo presente que la fuerza de reacción en el extremo O debe tener una dirección vertical, porque las otras dos fuerzas que actúan sobre el cuerpo son verticales.
Hagamos DCL del bloque teniendo presente que tanto el resorte como la cuerda vertical se encuentran "tensadas" y por tanto las fuerzas que actúan sobre el bloque debido a estos cuerpos se grafican "saliendo" del bloque.
Asumiendo que la longitud de la barra es 2L, apliquemos la segunda condición de equilibrio tomando momentos respecto del punto O: